Die Modellierung der Gesundheitskosten ist häufig problematisch, da diese nicht normal verteilt sind. Typischerweise gibt es eine große Anzahl von 0-Dollar-Beobachtungen (d. h. Personen, die keine Gesundheitsversorgung in Anspruch nehmen) und eine Kostenverteilung, die aufgrund einer unverhältnismäßig großen Anzahl von Personen mit sehr hohen Gesundheitskosten unter den Nutzern der Gesundheitsversorgung stark nach rechts verzerrt ist. Diese Beobachtung ist Gesundheitsökonomen wohlbekannt, für Modellierer erschwert jedoch die Zuordnung der Krankheitskosten zu bestimmten Gesundheitszuständen. Beispielsweise können die Kosten für die Krebsbehandlung je nach Krankheitsstadium und dem Fortschreiten des Krebses variieren. Die Kosten einer Herz-Kreislauf-Erkrankung unterscheiden sich, wenn der Patient einen Myokardinfarkt hat.
Ein Artikel von Zhou et al. (2023) bietet ein schönes Tutorial zur Kostenschätzung mit Krankheitsmodellzuständen unter Verwendung verallgemeinerter linearer Modelle. Das Tutorial enthält die wichtigsten Schritte.
Schritt 1: Vorbereiten des Datensatzes:
Der Datensatz erfordert normalerweise die Berechnung der Kosten für diskrete Zeiträume. Wenn Sie beispielsweise Schadensdaten haben, verfügen Sie möglicherweise über Informationen zu den Kosten nach Datum, für Analysezwecke benötigen Sie jedoch möglicherweise einen Datensatz mit Kosteninformationen nach Person (Zeilen), wobei die Spalten die Kosten nach Jahr (oder Monat) angeben. Alternativ könnten Sie die Beobachtungseinheit als Personenjahr (oder Personenmonat) festlegen und jede Zeile wäre ein separater Personenjahr-Datensatz. Als nächstes müssen die Krankheitszustände spezifiziert werden. In jedem Zeitabschnitt wird die Person einem Krankheitszustand zugeordnet. Zu den Herausforderungen gehört die Bestimmung, wie granular die Zustände sein sollen (z. B. nur MI vs. Timing seit MI) und wie mit Szenarien mit mehreren Zuständen umgegangen werden soll. Wenn Daten zensiert werden, kann man (i) eine Kovariate hinzufügen, um anzuzeigen, dass Daten zensiert werden, oder (ii) Beobachtungen ausschließen mit Teildaten. Wenn Kostendaten fehlen (der Patient jedoch nicht anderweitig zensiert wird), können mehrere Imputationsmethoden verwendet werden. Die Bildung der Analysezeiträume erfordert eine Zuordnung zur Zykluslänge des Entscheidungsmodells, einen angemessenen Umgang mit der Zensur und möglicherweise eine Datentransformation. Ein Beispieldatensatz ist unten dargestellt.
Schritt 2: Modellauswahl:
Das Papier empfiehlt die Verwendung eines zweiteiligen Modells mit einem Rahmen für ein verallgemeinertes lineares Modell (GLM), da OLS-Annahmen bezüglich Normalität und Homoskedastizität in den Residuen häufig verletzt werden. Mit dem GLM wird der erwartete Kostenwert nichtlinear transformiert, wie gezeigt in der Formel unten. Sie müssen sowohl eine Linkfunktion als auch die Verteilung des Fehlerterms schätzen. „Die beliebtesten (Kombinationen aus Verknüpfungsfunktion und Verteilung) für Gesundheitskosten sind die lineare Regression (Identitätsverknüpfung mit Gauß-Verteilung) und die Gamma-Regression mit einer natürlichen Logarithmusverknüpfung.)
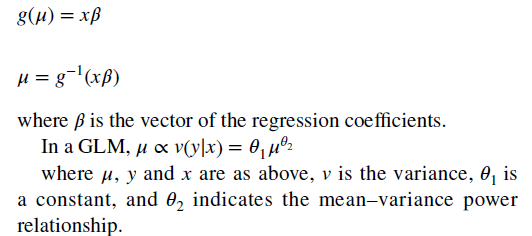
Um das GLM mit einem zweiteiligen Modell zu kombinieren, schätzt man einfach die obige Gleichung für alle positiven Werte und berechnet dann ein Logit- oder Probit-Modell für die Wahrscheinlichkeit, dass eine Person positive Kosten hat.
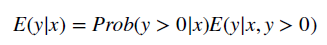
Schritt 3: Auswahl des endgültigen Modells.
Bei der Modellauswahl muss zunächst berücksichtigt werden, welche Kovariaten in die Regression einbezogen werden, die durch schrittweise Auswahl unter Verwendung einer vorab festgelegten statistischen Signifikanz ermittelt werden kann. Dies kann jedoch zu einer Überanpassung führen. Zu den alternativen Kovariaten-Auswahltechniken gehören die schrittweise Bootstrapping-Auswahl und bestrafte Techniken (z. B. Kleinster-Winkel-Auswahl- und Schrumpfungsoperator, LASSO). Auch Interaktionen zwischen Kovariaten könnten berücksichtigt werden. Die Gesamtanpassung kann anhand des mittleren Fehlers, des mittleren absoluten Fehlers und des quadratischen Mittelfehlers bewertet werden (letzterer wird am häufigsten verwendet). Besser passende Modelle weisen kleinere Fehler auf.
Schritt 4: Modellvorhersage
Während Kostenprognosen einfach durchzuführen sind, ist der Einfluss des Krankheitszustands auf die Kosten komplexer. Die Autoren empfehlen Folgendes:
Für ein einteiliges nichtlineares Modell oder ein zweiteiliges Modell können mithilfe der recycelten Vorhersage marginale Effekte abgeleitet werden. Es umfasst die folgenden zwei Schritte: (1) Führen Sie zwei Szenarien für die Zielpopulation durch, indem Sie den interessierenden Krankheitszustand auf (a) vorhanden (z. B. wiederkehrender Krebs) oder (b) nicht vorhanden (z. B. kein erneutes Auftreten von Krebs) festlegen. (2) Berechnen Sie die Differenz der durchschnittlichen Kosten zwischen den beiden Szenarien. Standardfehler der Mittelwertdifferenz können mithilfe von Bootstrapping geschätzt werden.
Die Autoren liefern auch ein anschauliches Beispiel für die Anwendung dieses Ansatzes zur Modellierung der Krankenhauskosten im Zusammenhang mit kardiovaskulären Ereignissen im Vereinigten Königreich. Die Autoren stellen auch den Beispielcode in R zur Verfügung, den Sie hier herunterladen können.